 The gas particles move so freely that is why it is difficult to learn about the characteristics of the gas. The simplification of the problem for studying the gas is to create a definition and scope boundary about the ideal gas. The ideal gas is a gas that has the ideal special characteristic.
The gas particles move so freely that is why it is difficult to learn about the characteristics of the gas. The simplification of the problem for studying the gas is to create a definition and scope boundary about the ideal gas. The ideal gas is a gas that has the ideal special characteristic.
Those characteristics are having perfect resilient collision, Newton’s laws of motion is applied, no force between particles, moving in all directions and spread evenly. In real life, the ideal gas never existed. Here we are going to explain about gas laws definition, formulas, and examples.
Ideal Gas Characteristics
- Consists of molecules (particles) in large numbers of atoms or groups of atoms
- Gas particles always move randomly with any direction, but all of them move in all directions at various speeds.
- Individual gas particles or containers are evenly distributed throughout the room or container.
- The gas particle meets Newton’s Law of Motion (read: The example of Newton’s law 3 and its explanation)
- Collision between molecules or cubicles that hit with gas is a perfect collision that occurred in a short time.
Ideal Gas Equations
The magnitude component involved in forming equations relating to some of the laws of an ideal gas by some scientists:
- Pressure (P)
- Volume (V)
- Absolute Temperature (T)
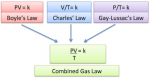
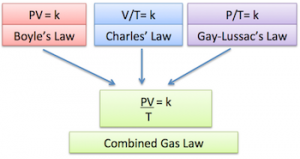
The scientists who studied the ideal gas created several laws and equations that became the basis of the ideal gas which is Robert Boyle with Boyle’s Law, Jacques Chares with Charles Law, Joseph Gay Lussac with Gay Lussac Law. From those three scientists, born laws and combined equation of the three laws which is known by Boyle-Gay Lussac Law which we commonly use today. Here’s an explanation of each law we learn about the ideal gas.
1. Boyle’s Law
The law was discovered by a scientist Robert Boyle (1627-1691) known as Boyle’s Law. Boyle’s law reveals that:
“The result of multiplication between pressure and volume if the temperature remains constant.”
The law can be written with the following equation:
P V = constant or P1 V1 = P2 V2
Information :
P1 = initial gas pressure (N / m2)
V1 = initial gas volume (m3)
P2 = final gas pressure (N / m2)
V2 = final volume (m3)
The relationship of pressure and volume at fixed temperature to Boyle’s law can be illustrated in the following graphic form.
Problems example:
The temperature of the gas in the enclosed space at 27 ° C has a pressure of 5 x 105 Pa. The initial volume is V which is then pressed to a volume of ¼ V. What is the final pressure?
Resolution:
Is known :
T1 = (27 + 273) K = 300 K
V1 = V
V2 = ¼ V
P1 = 1.5 x 105 Pa
Asked: P2 ………….?
Answer:
P1. V1 = P2. V2
(1.5 x 105). V = P2. (¼V)
P2 = 5 x 105 Pa
So the final pressure is 5 x 105 Pa
2. Charles’s Law
The investigation was continued by Jacques Charles (1747-1823). From the results of his investigation it became known that Charles Law states that:
“If the gas pressure in a closed space is kept constant, then the gas volume is directly proportional to the temperature.”
The form of the statements of the charles law can be written by the equation:
V / T = Constant or V1 / T1 = V2 / T2
Information:
V1 = initial gas volume (m3)
V2 = final gas volume (m3)
T1 = initial absolute temperature (K)
T2 = final absolute temperature (K)
Based on the Charles Law equation the relationship of temperature and volume can be described in the following graph
The graph applies to all gas types. The temperature is expressed in Kelvin (K). The basis for this Kelvin scale is absolute zero which is the lowest temperature that the gas reaches -273 ° C or 0 K. So that all types of gases can not be cooled again less than absolute zero.
3. Gay Lussac’s Law
One more scientist that influences the ideal gas equation that observes the relationship of pressure and temperature of the gas to the fixed volume is Joseph Gay Lussac. And produce a statement or law known as Gay Lussac’s Law. The statements are as follows:
“The gas pressure is directly proportional to the gas temperature if the volume in the enclosed space is fixed”.
The statement can be written with the following equation:
P / T = Constant or P1 / T1 = P2 / T2
Information :
P1 = initial gas pressure (N / m2)
P2 = final gas pressure (N / m2)
T1 = initial absolute temperature (K)
T2 = final absolute temperature (K)
The relationship equation between pressure and temperature in Gay Lussac Law can be expressed in the graph as follows:
4. Boyle’s Law – Gay Lussac
The result of the merger of the three laws of the above scientists will be obtained in the equation which became known as Boyle-Gay Lussac’s Law. The incorporation of the law can be expressed by the following equation:
P.V / T = constant Or P1V1 / T1 = P2.V2 / T2
Information :
P1 = initial gas pressure (N / m2)
P2 = final gas pressure (N / m2)
T1 = initial absolute temperature (K)
T2 = final absolute temperature (K)
V1 = initial gas volume (m3)
V2 = final gas volume (m3)
Problems example:
The ideal gas temperature of 47 oC as much as 4 liters has a pressure of 1 atmosphere. What is the ideal gas pressure if the temperature is increased to 57 ° C and the volume is 3.3 liters!
Resolution:
Is known:
V1 = 4 liters
V2 = 3.3 liters
P1 = 1 atm
T1 = 47 oC = 47 + 273 = 320 K
T2 = 57 oC = 47 + 273 = 330 K
Asked: P2 ………….?
Answer:
P1.V1 / T1 = P2.V2 / T2
(1 x 4) / 320 = P2 (3,3) / 330
0.0125 = P2 (0.01)
P2 = 1.25 atm
The final ideal gas pressure is 1.25 atm
5. Ideal Gas General Law
Each gas has different characteristics if the pressure, volume and temperature of the gas are different although the number of molecules is the same. Therefore, a constant is called the Boltzman constant (k).
So the equation can be acquired as follows:
PV = NkT or PV = n NA k T
Information:
N = number of gas molecules
NA = Avogadro number (6.02 x 1023 molecule / mol)
n = number of moles of gas
k = Boltzman constant (1.38 x 1023J / K)
NA & k are called the common gas constants denoted by R. So the equation can be written to be:
PV = nRT
Information:
R = common gas constants
=8,314 J / mol K
= 0.082 L atm / mol K
The last equation is then called Ideal Gas Equation.
m = 16 gram
Mr O2= Ar O x 2 = 32
P = 2 x 105Pa
R = 8,31 J/mol.K
V = 5 liter = 5 x 10-3 m3
Asked: T….?
Answer:
n = M/Mr = 16/32
P . V = n . R . T
T = P.V/n.R
T = (2 x 105)(5x 10-3)/(0,5)(8,31)
T = 2,406 x 102K
That’s all about the complete and clear explanation about gas laws definition, formulas, and examples. Happy studying chemistry!